Esperanto · Español (WIP) · English
Tiuj ĉi notoj estas mallonga superrigardo pri baza kombinatoriko uzante "la dekduoblan manieron," kreita de la matematikisto Gian-Carlo Rota por montri ke multaj kombinatorikaj problemoj baze estas variaĵo de la demando "kiom da funkcioj ekzistas inter du finecaj aroj?" Kiel ĉiam, eble estas eraroj, kaj korektoj estas ŝatataj.
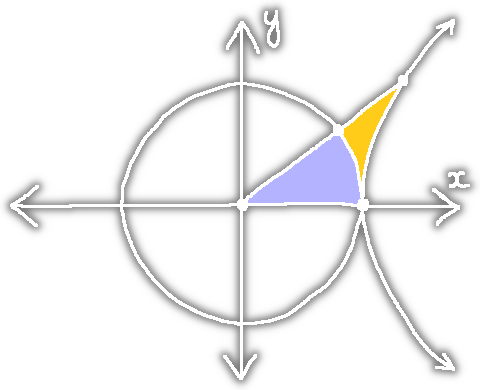
Tiu ĉi paĝo celas zorgeme kaj nature defini la cirklajn kaj hiperbolajn funkciojn. Mi ankaŭ volas montri ke ili estas tre similaj. Mi skribas tiun ĉi paĝon ĉar plej da la priskriboj de la cirklofunkcioj aŭ estas tute malnaturaj aŭ kaŝas cirklorezonon.
Ekzemple, ili eble diras ke π estas kvociento de arkomezuro kaj duradiuso, sed ili neniam klarigas kiel oni scias ke tiu kvociento neniam ŝanĝas laŭ tiuj mezuroj, aŭ kiel oni difinu arkomezuron. Fari la lastan aferon postulas uzi amasaĵon (integralon). Aliflanke, estas multaj priskriboj kiu simple ne provas uzi naturan difinon kaj nur ĵetas al oni serion de Tejlor, kiu postulas ke oni difinu limvalorojn.
Pro tiuj kialoj, ĝenas min kiam uloj diras ke oni «devas lerni trigonometrion antaŭ senfineconan kalkulon.» La norma lerneja studoplano simple estas malsciema. La filmetoj de Wildberger, kaj ankaŭ la serio de Daniel Rubin «Tricky Parts of Calculus» (Malfacilaj Aferoj de Kalkulo) multe inspiris min skribi tiun ĉi paĝon.