Esperanto · Español (WIP) · English
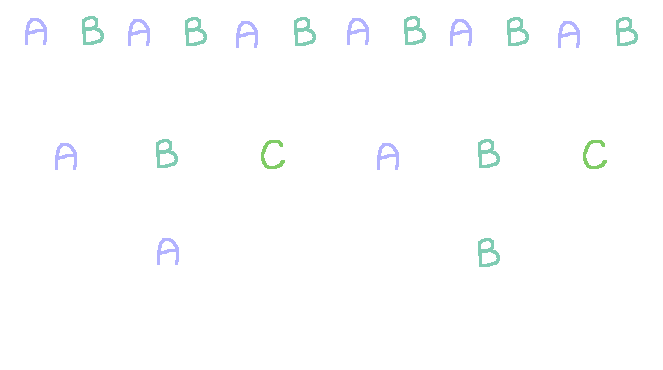
These notes give a brief overview of basic combinatorics from the perspective of the twelvefold way, which was created by the mathematician Gian-Carlo Rota in order to showcase that many combinatorial problems boil down to some variation of asking how many functions there are from one set to another. As always, there might be errors, and corrections are appreciated.
Most treatments of differential forms out there are completely undecipherable, and even when bits and pieces do make sense, they still leave you wondering what ever happened to dx and dy just being tiny nudges. My hope with these notes is to remedy this sort of thing.
These notes couldn't be possible without Michael Penn's excellent playlist on differential forms on YouTube, as it is the only resource I could find which makes any sense whatsoever. With the exception of Chapter I, these notes are basically just a reinterpretation of his approach.
My understanding of differential forms is still incomplete. This is effectively an open notebook at this time. If you see any mistakes, let me know! Also, I'm not even going to attempt to touch manifolds because they scare me.
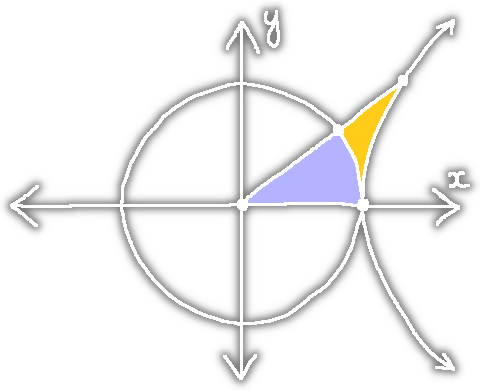
The goal of this page is to define the circular and hyperbolic functions carefully yet naturally. I also want to show just how similar they really are. I'm writing this because most treatments of the circles and the circular functions either hide some circular reasoning or are completely unmotivated.
For example, they might say that π is a ratio involving an arclength, but it is never explained how we know this ratio is always the same, or how to define arclength. Doing the latter requires some form of integration. On the other hand, you have treatments that give up on a natural definition completely and just throw some power series at you, which also requires limits anyways.
Incidentally, this is why I find it really annoying when people say you "have to learn trigonometry before calculus." In reality, the standard curriculum is just ignorant. Wildberger's videos, as well as Daniel Rubin's Tricky Parts of Calculus were big inspirations for this project.