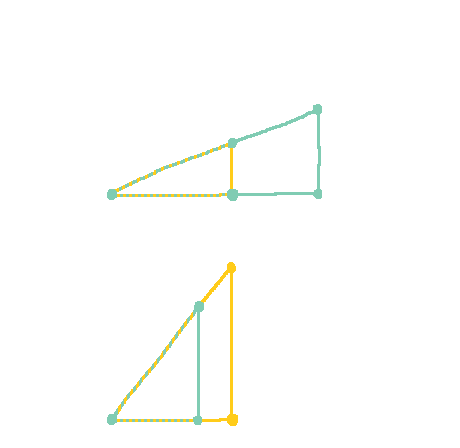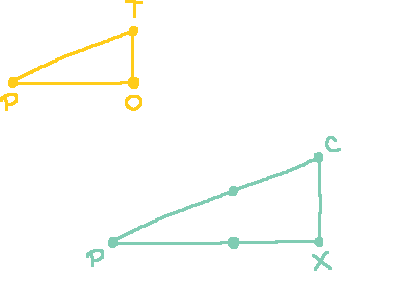Circular Functions

1. Parametrizing the Unit Circle
2. Areas and Circumferences
3. Defining the Circular Functions

Hyperbolic Functions

1. Measuring the Unit Hyperbola
2. Defining the Hyperbolic Functions

Our immediate objective before defining the circular functions is to find a way to describe the unit circle analytically. Rather than directly using the traditional $x^2 + y^2 = 1$ which follows immediately from the Pythagorean Theorem and the fact that every point on a circle is the same distance away from the center, we will use a parametrization of the unit circle.

The parametrization works like this: when a chord is made from the point (-1, 0) to any other point on the unit circle, the chord must cross the y-axis at some y-coordinate $t$. The coordinates of the point on the unit circle where the chord goes are then rational functions of $t$.

Proposition I: The unit circle is rationally parametrized by:

$$x = \frac{1 - t^2}{1 + t^2}$$ $$y = \frac{2t}{1 + t^2}$$

Where $t$ is the $y$-coordinate of the point where a chord from the point $(-1, 0)$ to some point on the unit circle crosses the $y$-axis.

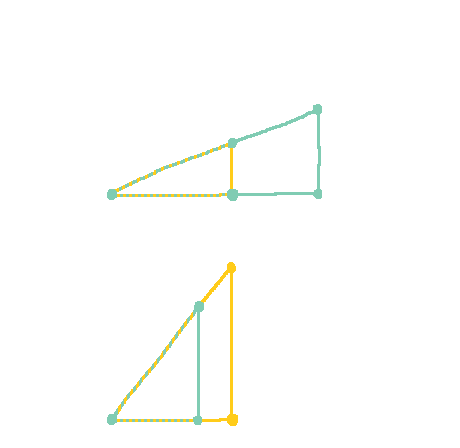
Proof: Let O be the origin. Draw the chord from the point P $= (-1, 0)$ to any point C on the circle. Let T be the point with y-coordinate $t$ where this chord PC crosses the y-axis. Drop the altitude CX perpendicular to the $x$-axis. Observe that the triangles PTO and PCX are similar triangles. That is, they form the same slope. This means there must exist some scaling factor $s(t)$ from PTO to PCX. Also observe that PO = 1 since it is a radius of the circle.

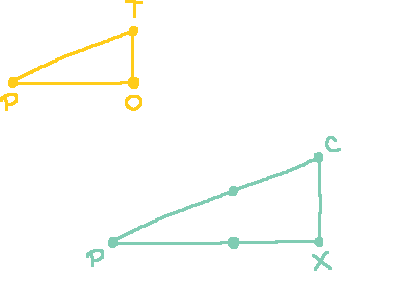
The diagram above shows the lengths of triangle PTO before being scaled up to triangle PCX. In particular, note that $1+x = s(t)$ and $y = s(t)\,t$. Applying the Pythagorean Theorem to triangle PCX then gives us:

$$\begin{align*} s(t)^2\,(1+t^2) &= (1+x)^2 + y^2\\ &= x^2 + 2x + 1 + y^2\\ &= 2x + 2\\ &= 2(x + 1)\\ &= 2s(t)\\ \Rightarrow s(t) &= \frac{2}{1+t^2} \end{align*}$$

The result then follows from straightforward manipulation. $\square$

This parametrization can be immediately generalized to all circles by simply multiplying the $x$ and $y$ coordinates by some radius $r$. It is not hard to check that this does in fact give a circle. We only need to check that this satisfies $(r\,x(t))^2 + (r\,y(t))^2 = r^2$.

With a parametrization for the circle under our belt, our next endeavor shall be to find the circumference of the circle and its area. Both of these are most easily stated in terms of angles. We will define angle measure using arclengths of the unit circle. The rationale for this will be made clear later. Recall that the arclength formula is:

$$L = \int_{a}^{b} \sqrt{\left(\frac{dx}{dt}\right)^2 + \left(\frac{dy}{dt}\right)^2} dt$$

In order to make use of this arclength formula, we first need to take derivatives of each of the functions in the parametrization. Fortunately rational functions don't require any fancy tricks. Despite this, the result of the calculation turns out to be rather interesting.

Proposition II: The derivatives of the functions defining the parametrization of a circle of radius $r$ are given by:

$$\frac{d(rx)}{dt} = -r\,s(t)\,y(t)$$ $$\frac{d(ry)}{dt} = r\,s(t)\,x(t)$$

Proof: See Exercise II. $\square$

This will allow us to compute the arclength of a unit circle from 0 to some chosen y-coordinate $t_0$ using the rational parametrization. We will denote this by $\theta(t)$. Using the identity $x^2 + y^2 = 1$, we conclude:

$$\begin{align*} \sqrt{(dx/dt)^2 + (dy/dt)^2} &= \sqrt{ s(t)^2\,y(t)^2 + s(t)^2\,x(t)^2} \\ &= s(t) \sqrt{y(t)^2 + x(t)^2} \\ &= s(t) \\ &= 2/({1 + t^2}) \end{align*}$$

Which leaves us with:

$$\theta(t) = \int_0^t \frac{2\,du}{1 + u^2}$$

Exercises

Exercise 1.1.1: Complete the proof of Proposition I.

Exercise 1.1.2: Prove Proposition II.

Exercise 1.1.3: Show that $\theta$ is injective.

Observe above that when we scale the parametrization of the unit circle by a radius $r$ to parametrize a general circle, The circular sector obtained by allowing the parameter to vary from $0$ to $t$ appears to cover the same angle as the unit circular sector obtained by allowing the parameter to vary within in the same interval. We use this observation to motivative the following definition:

Definition: Given a particular radius, the circular sector of angle $\varphi \in \text{im } \theta$ is the portion of the circle obtained by letting the rational parametrization of the circle vary from $0$ to $t$, where $t \in \mathbb{R}$ satisfies $\varphi = \theta(t)$.

The existence of such a unique $t$ is guaranteed by the fact that $\theta$ is an injection. With this definition in place, we can precisely state the formulas for circular area and arclength as theorems.

Proposition III: Let $r \in \mathbb{R}^+$ be the radius of a circle and let $\theta(t) \in \text{im } \theta$ for some $t \in \mathbb{R}$ be an angle. Then the arclength $L(t)$ of the corresponding circular sector is given by $r\theta(t)$, and the area of the corresponding circular sector $A(t)$ is given by $\frac{1}{2}r^2\theta(t)$

Proof: As before, when computing $\theta(t)$:

$$\begin{align*} \sqrt{(d(rx)/dt)^2 + (d(ry)/dt)^2} &= \sqrt{ r^2\,s(t)^2\,y(t)^2 + r^2\,s(t)^2\,x(t)^2} \\ &= r\,s(t) \sqrt{y(t)^2 + x(t)^2} \\ &= r\,s(t) \\ \end{align*}$$

So that by the arclength formula:

$$L(t) = \int_{0}^{t} rs(u)\,du = r \int_{0}^{t} s(u)\,du = r \theta(t)$$

Now, by the formula for the area of a parametric sector:

$$A = \frac{1}{2} \int_{a}^{b} x\frac{dy}{dt} - y\frac{dx}{dt} \,dt$$

The area of the circular sector is given by:

$$\begin{align*} A(t) &= \frac{1}{2} \int_{0}^{t} rx\frac{d(ry)}{du} - ry\frac{d(rx)}{du} \,du\\ &= \frac{1}{2} \int_{0}^{t} r^2 sx^2 + r^2 sy^2\,du\\ &= \frac{1}{2} \int_{0}^{t} r^2s\,du\\ &= \frac{1}{2} r^2 \int_{0}^{t} s\,du\\ &= \frac{1}{2} r^2 \theta(t)\\ \end{align*}$$

Which is the desired result. $\square$

Notice that these functions count areas and arcs under the x-axis as negative. This means that if we want to find the full area and circumference of a circle, we will need to either alter the range of integration to be from $-\infty$ to $\infty$, or multiply the functions we derived by 2 and then let $t \rightarrow \infty$. Doing the latter for area gives:

$$\begin{align*} A &= \lim_{t \rightarrow \infty} 2A(t)\\ &= \lim_{t \rightarrow \infty} 2 \frac{1}{2} r^2 \theta(t)\\ &= r^2 \lim_{t \rightarrow \infty} \theta(t) \end{align*}$$

And for circumference, we get:

$$\begin{align*} C &= \lim_{t \rightarrow \infty} 2L(t)\\ &= \lim_{t \rightarrow \infty} 2r \theta(t)\\ &= 2r \lim_{t \rightarrow \infty} \theta(t) \end{align*}$$

Recalling that the diameter of a circle is twice its radius, the equations above tell us that the ratio of a circle's circumference to its diameter is always the limit above. Thus, we define:

$$\pi = \lim_{t \rightarrow \infty} \theta(t)$$

Which means that the image of $\theta$ is the interval $(-\pi, \pi)$, and also leaves us with the classic formulas:

$$A = \pi r^2$$ $$C = 2\pi r$$

Exercises

Exercise 1.2.1: Prove that $\lim_{t \rightarrow \infty} \theta(t)$ exists and is less than 4.

Exercise 1.2.2: Using only properties of integration, explain why the integral representation of $\pi$ below agrees with the limit representation used above as a definition.

$$\pi = \int_{-\infty}^{\infty} \frac{du}{1 + u^2}$$

Intuitively, we define the circular or trigonometric functions as accepting as an input the length of an arc going counterclockwise along the unit circle from the point $(1, 0)$ and giving as an output the x and y coordinates of the point on which that arc ends. The picture of this definition is shown on the left.

This intuitive definition is usually presented without additional comment, which is usually fine for all practical purposes. However, our work in the previous act puts us in a good position to make this intuitive definition much more precise.

Since we now have a precise way to compute both angles and points on the unit circle in terms of the argument $t$ of the rational parametrization, we can define the circular functions using $t$:

Definition: The sine function $\sin: \mathbb{R} \rightarrow [-1, 1]$ and the cosine function $\cos: \mathbb{R} \rightarrow [-1, 1]$ are functions defined to be $2\pi$-periodic and satisfy the functional equations:

$$\sin(\theta(t)) = \frac{2t}{1+t^2}$$ $$\cos(\theta(t)) = \frac{1-t^2}{1+t^2}$$

This definition is conceptually identical to the unit circle definition. However, since it has more moving parts, it's worth stopping to make sure that we didn't screw anything up by putting it this way.

Recall that $\theta(t)$ is injective, and that its image is the interval $(-\pi, \pi)$. This means that for any real number $r \in (-\pi, \pi)$ there is some unique corresponding $t_0 \in \mathbb{R}$ such that $\theta(t_0) = r$.

This value $t_0$ may be plugged into the right side of the definitions if $r$ is plugged into one of the circular functions. Thus, the functional equation is a sensible way to define the circular functions over the whole interval $(-\pi, \pi)$.

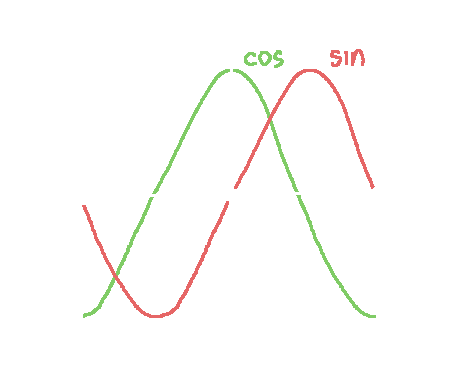
Since the interval $(-\pi, \pi)$ has a length of $2\pi$, imposing $2\pi$ periodicity does not lead to any conflict as to which values the circular functions have in $(-\pi, \pi)$, and thus the functions are successfully extended to all real numbers. Well, almost. We still haven't defined the functions at inputs which are odd integer multiples of $\pi$. To rectify this, we observe that:

$$\begin{align*} \lim_{\theta \rightarrow \pi} \sin(\theta) &= \lim_{t \rightarrow \infty} \sin(\theta(t))\\ &= \lim_{t \rightarrow \infty} \frac{2t}{1+t^2}\\ &= 0\\ \end{align*}$$

And analogously, that:

$$\begin{align*} \lim_{\theta \rightarrow \pi} \cos(\theta) &= \lim_{t \rightarrow \infty} \cos(\theta(t))\\ &= \lim_{t \rightarrow \infty} \frac{1-t^2}{1+t^2}\\ &= -1\\ \end{align*}$$

So we simply take these to be the values of the circular functions at $\pi$ as part of the definition, as they are the values that keep the functions continuous. Periodicity takes care of all other odd integer multiples of $\pi$. With this final stipulation, the circular functions become defined as desired. We are now ready to prove the following important result:

Proposition IV: The sine and cosine functions are differentiable, with derivatives:

$$\frac{d}{d\theta} \sin(\theta) = \cos(\theta)$$ $$\frac{d}{d\theta} \cos(\theta) = -\sin(\theta)$$

Proof: The differentiability of sine and cosine follow from the fact that $x(t)$, $y(t)$, and $\theta(t)$ are all differentiable. Taking derivatives with respect to $t$ on both sides of the definition of sine, we can use the Chain Rule to compute:

$$\begin{align*} \frac{d}{dt}\sin(\theta) &= \frac{dy}{dt}\\ \frac{d}{d\theta}\sin(\theta)\,\frac{d\theta}{dt} &= s(t)\,x(t)\\ \frac{d}{d\theta}\sin(\theta)\,s(t) &= s(t)\,x(t)\\ \frac{d}{d\theta}\sin(\theta) &= x(t)\\ &= \cos(\theta) \end{align*}$$

This gives us the derivative over $(-\pi, \pi)$, and it extends to almost all of the reals by periodicity. The result is extended to odd integer multiples of $\pi$ by a theorem that says any function that is differentiable everywhere around a point is also differentiable at that point with matching derivatives (See Spivak's Calculus, citation will be provided later). The derivative of the cosine function is shown to be negative sine in a similar way. $\square$

Now that we've gotten the basic facts about the circular functions established, it is time to concern ourselves with the circular functions. This process is extremely similar to setting up the circular functions, and where it differs it is usually simpler. The unit hyperbola we are concerned with is described by the equation $x^2 - y^2 = 1$. As before, we can leverage a triangle similarity to come up with a rational parametrization for this curve. Everything is more or less analogous to the circular case, and the calculations are extremely similar, just that we have a minus instead of a plus.

It should be kept in mind that although not shown in the picture to save space, the hyperbola continues below the x-axis by reflection as described by the equation. Anyways, the triangle similarity is the same as before. Here is the diagram again for convenience.

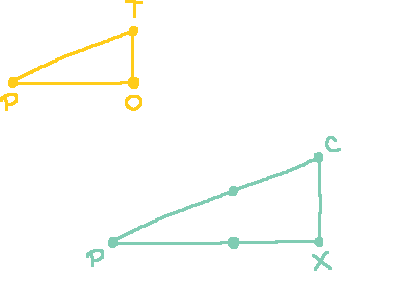
The diagram above shows the lengths of triangle PTO before being scaled up to triangle PCX. In particular, note that $1+x = s(t)$ and $y = s(t)\,t$. Applying the Pythagorean Theorem to triangle PCX then gives us:

$$\begin{align*} s(t)^2\,(1+t^2) &= (1+x)^2 + y^2\\ &= x^2 + 2x + 1 + y^2\\ \Rightarrow s(t)^2\,(1+t^2) - 2y^2 &= x^2 + 2x + 1 - y^2\\ &= 2(x + 1)\\ &= 2s(t)\\ \Rightarrow s(t)\,(1+t^2) - 2s(t)t^2 &= 2\\ \Rightarrow s(t)\,(1-t^2) &= 2\\ \Rightarrow s(t) &= \frac{2}{1-t^2} \end{align*}$$

Basic algebra then once again leaves us with the following parametrization, which for $t \in (-1, 1)$ gives us the entire unit hyperbola to the right of the y-axis:

$$x = \frac{1+t^2}{1 - t^2}$$ $$y = \frac{2t}{1 - t^2}$$

And differentiation rules, as is left for the reader to check, tell us that:

$$\frac{dx}{dt} = s(t)y(t)$$ $$\frac{dy}{dt} = s(t)x(t)$$

Sadly, the calculations for arclength are not as nice as they were last time. However, keep in mind that in the unit circle, we had $A(t)=\frac{1}{2}\theta(t)$ (Proposition III), which will be useful when defining the hyperbolic functions. In the meantime, we can compute the area of a parametric sector as before without issue. Using $x^2 - y^2 = 1$, we get:

$$\begin{align*} A(t) &= \frac{1}{2} \int_{0}^{t} x\frac{d(y)}{du} - y\frac{d(x)}{du} \,du\\ &= \frac{1}{2} \int_{0}^{t} sx^2 - sy^2\,du\\ &= \frac{1}{2} \int_{0}^{t} s\,du\\ &= \frac{1}{2} \int_{0}^{t} s\,du\\ &= \int_{0}^{t} \frac{du}{1-u^2}\,du\\ \end{align*}$$